Principal connection
It is a particular case of connection on a fiber bundle.
Definition
A connection on a principal $G$-bundle $P\stackrel{\pi}{\rightarrow}M$, with $dim(M)=n$, is a $n$-dimensional distribution (named horizontal distribution)
$$H:u\mapsto H_u P\subseteq T_u P$$
on $P$ such that the following conditions hold for every $u\in P$:
- $T_u P=V_u P \oplus H_u P$, where $V_u P=Ker((d\pi)_u)$.
- $H_{\rho_g(u)} P=(d\rho_g)_u(H_u P)$, for every $g\in G$, and being $\rho_g$ the right action of $g$ in $P$
Here $VP$ is the vertical bundle.
The simplest example of a connection is the trivial connection on the trivial bundle $P=M\times G$, that is, $$H_{(m,g)} P=T_m M \subseteq T_{(m,g)} P.$$
Connection 1-form
It can be shown ([Vakar 2011]), without much difficulty, that a connection can be alternatively defined as a 1-form $\omega \in \Omega^1(P) \otimes \mathfrak{g}$, being $\mathfrak{g}$ the Lie algebra of $G$, that satisfies:
- $\omega(\tilde{A})=A$, for every $A\in \mathfrak{g}$ and being $\tilde{A}$ the fundamental vector field of $A.$
- For every $g\in G$ the following diagram commutes:
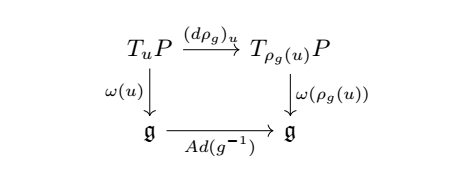
being $G \stackrel{\mathrm{Ad}}{\longrightarrow} G L(\mathfrak{g})$ the adjoint representation of $G$. This can be written
$$ \rho_g^*(\omega)=Ad_{g^{-1}} \omega $$which is the same expression that we find for the Maurer-Cartan form (see Maurer-Cartan form#MC form and left and right actions). The connection is then an extension of the Maurer-Cartan form of the bundle to the whole $T_uP$ but the values are still in $\mathfrak{g}$. A Cartan connection is similar, but the values are taken in a bigger Lie algebra.
Observe that given the horizontal distribution $H$ we can construct the associated 1-form $\omega$ by projecting every vector $X \in T_u P$ to $V_u P$ and identifying the latter with $\mathfrak{g}$ by using the Maurer-Cartan form and any trivialization (see [Belgun 2020] for more details). Conversely, given a connection by the 1-form $\omega$, we recover the horizontal distribution by means of
$$ H_{u} P:=\left\{X \in T_{u} P \mid \omega(u)(X)=0\right\} $$Idea
See the idea in the particular case of affine connection.
Another characterization
But connections can be characterized in one more way. Given an atlas $\{(U_{\alpha},\psi_{\alpha})\}_{\Lambda}$ for the $G$-bundle $P\stackrel{\pi}{\rightarrow}M$ and the connection defined by $\omega$, we can use the collection of distinguished local $G$-frames (local sections) $p_{\alpha}:U_{\alpha} \rightarrow P$ (see principal bundle#Alternative approach) to define the family of local 1-forms
$$ \omega_{\alpha}=p_{\alpha}^*(\omega) \in \Omega^1(U_{\alpha}) \otimes \mathfrak{g} $$satisfying
$$ \omega_{\beta}(m)=Ad\left(g_{\alpha\beta}(m)^{-1}\right) \omega_{\alpha}(x)+\Theta_{\alpha\beta}(m), \tag{!} $$ $$ \forall m \in U_{\alpha \beta} \text { and } \forall \alpha, \beta \in \Lambda $$where $\Theta_{\alpha\beta}$ denote $g_{\alpha\beta}^*(\Theta)$, being $\Theta$ the Maurer-Cartan form. Every $\omega_{\alpha}$ is called a Yang-Mills field (see [Schuller 2013] page 185).
Reciprocally, any collection $\{(U_{\alpha},\psi_{\alpha},\omega_{\alpha})\}$, being $\{(U_{\alpha},\psi_{\alpha})\}$ an atlas for the bundle $P\stackrel{\pi}{\rightarrow}M$, defines a connection on it if $\{\omega_{\alpha}\}$ satisfies condition (!) (see [Marathe 1992] for a proof).
The idea behind Yang-Mills fields is what follows. The local section $p_{\alpha}$ is a moving frame, that is, a choice of a $G$-frame for every point $m\in U$. The 1-form $p_{\alpha}^*(\omega)$ evaluated on a vector $v\in T_m M$ tells us how the frame varies when we move in the direction $v$ (assuming the notion of derivative provided by the connection $\omega$). But this "variation" is measured in terms of elements of $\mathfrak{g}$.
Exterior covariant derivative
An important feature is exterior covariant derivative.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: